Schau genau hin! Mathematiker haben eine neue 13-seitige Form geschaffen, die endlos gekachelt werden kann, ohne dass sich ein Muster wiederholt. Sie nennen ihn „Einstein“.
Seit Jahrzehnten fragen sich Mathematiker, ob es möglich wäre, eine einzige spezielle Form zu finden, die eine Oberfläche perfekt kachelt, ohne Lücken zu hinterlassen oder Überlappungen zu verursachen, ohne das Muster zu wiederholen. Natürlich ist dies eine Kleinigkeit mit einem sich wiederholenden Muster – schauen Sie sich nur Ihren Badezimmer- oder Küchenboden an, der wahrscheinlich aus einfachen rechteckigen Fliesen besteht. Wenn Sie den Boden aufheben und herumbewegen würden (in der Mathematik als „Übersetzung“ bezeichnet), könnten Sie eine Position finden, an der der Boden genau so aussah wie zuvor, was beweist, dass es sich um ein sich wiederholendes Muster handelt.
1961 sagte der Mathematiker Hao Wang voraus, dass aperiodische Bischöfe oder Bischöfe, die nicht zu einem sich wiederholenden Muster werden, unmöglich seien. Aber sein Schüler Robert Berger übertraf ihn und fand eine Reihe von 20.426 Formen, die sich bei sorgfältiger Anordnung nie wiederholen. Dann grenzte er das auf einen Satz von 104 Stück ein. Das bedeutet, dass Sie, wenn Sie ein Set dieser Fliesen kaufen würden, sie auf Ihrem Küchenboden anordnen könnten und niemals ein sich wiederholendes Muster finden würden.
In den 1970er Jahren fand der mit dem Nobelpreis ausgezeichnete Physiker Roger Penrose einen Satz von nur zwei Teilen, die in einem sich nicht wiederholenden Muster, das heute als Penrose-Kacheln bekannt ist, zusammen angeordnet werden konnten.
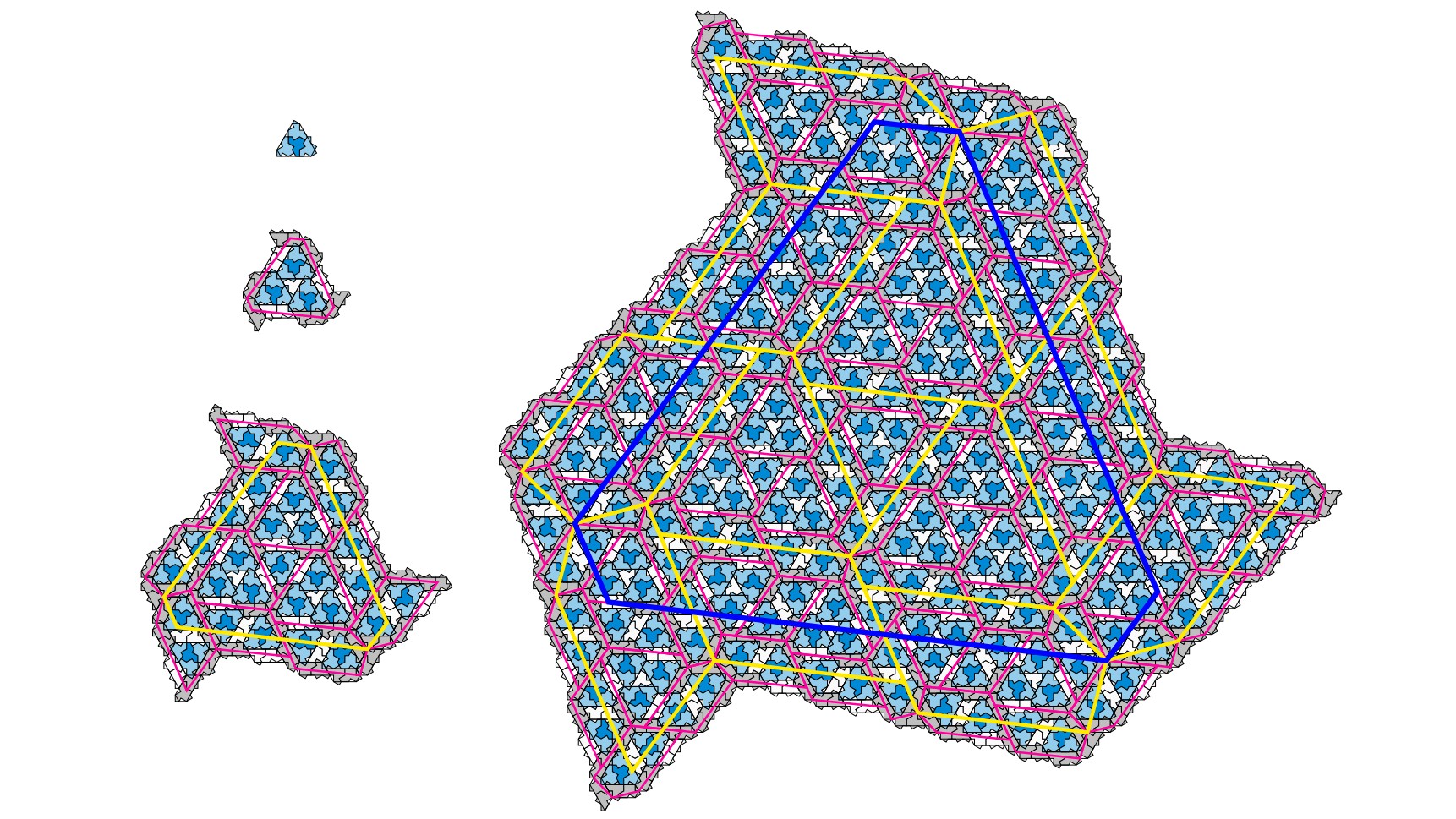
Seitdem suchen Mathematiker auf der ganzen Welt nach dem heiligen Gral der nichtperiodischen Kachelung, der „Einstein“ genannt wird. Das Wort kommt nicht von berühmter albert Aber aus der deutschen Übersetzung seines Nachnamens: ein Stein. Kann eine einzelne Fliese – ein einzelner „Stein“ – einen zweidimensionalen Raum füllen, ohne das Muster zu wiederholen, das er macht?
Die Antwort wurde gerade von David Smith, einem pensionierten Grafiker aus East Yorkshire, England, entdeckt. Wie sind Sie auf diese tolle Lösung gekommen? „Ich spiele immer herum und experimentiere mit Formen“, sagte Smith. New Yorker Zeiten (Öffnet in einem neuen Tab). „Es ist immer gut, Hand anzulegen. Es kann ziemlich meditativ sein.“
Smith und seine Kollegen nannten die neue Form „Hut“, weil sie vage einem Fedora ähnelte. Obwohl Mathematiker von der Figur mit 13 Seiten wissen, haben sie sie nie als Kandidat für aperiodisches Kacheln angesehen.
„In gewisser Weise hat er die ganze Zeit dort gesessen und darauf gewartet, dass ihn jemand findet.“ Marjorie Senechal (Öffnet in einem neuen Tab)Ein Mathematiker vom Smith College, der nicht an der Studie teilnahm, sagte gegenüber The Times.
Smith arbeitete eng mit zwei Informatikern und einem anderen Mathematiker zusammen, um zwei Beweise zu entwickeln, die zeigen, dass der „Hut“ ein nicht periodisches Einstein-Monogramm ist. Ein Beweisstück stützte sich auf den Aufbau immer größerer hierarchischer Gruppen von Quadraten und zeigte, dass sich das Muster nie wiederholt, wenn die Oberfläche wächst. Andere Beweise stützten sich auf die Entdeckung des Teams, dass es nicht nur ein solches Quadrat gab, sondern eine unendliche Vielfalt verwandter Formen, die alle ausreichen konnten. Teamblatt erhältlich unter arXiv-Prepress-Server (Öffnet in einem neuen Tab) Aber es wurde noch nicht begutachtet, und die Beweise wurden noch nicht geprüft.
Diese Arten von nicht periodischen Dächern sind mehr als nur eine mathematische Kuriosität. Sie dienen zum Beispiel als Sprungbrett für Kunstwerke wie die Penrose-Fliesen Gefunden im Salesforce Transit Center (Öffnet in einem neuen Tab) in San Francisco und enthüllt, dass einige mittelalterliche islamische Mosaiken ähnliche, sich nicht wiederholende Muster verwendeten.
Nichtperiodische Bischöfe helfen auch Physikern und Chemikern, Struktur und Verhalten zu verstehen QuasikristalleStrukturen, in denen Atome angeordnet sind, aber kein sich wiederholendes Muster aufweisen.









More Stories
Die deutsche Luft- und Raumfahrtindustrie steht vor dem Ende des Typhoon-Programms
Airbus erhält 2,1 Milliarden Euro für den Aufbau eines deutschen militärischen Kommunikationssystems
RFA, ATMOS und Yuri kündigten den Mikrogravitationsdienst „Eva“ an